代码随想录算法训练营第16天

今日任务

● 104.二叉树的最大深度 559.n叉树的最大深度 ● 111.二叉树的最小深度 ● 222.完全二叉树的节点个数

链接：https://docs.qq.com/doc/DUHBQRm1aSWR4T2NK (opens in a new tab)

104.二叉树的最大深度

自己想法

可以用递归，也可以用迭代，迭代的话就是（昨天练习的）层序遍历，每遍历一层，深度加一。

递归方法中，本题可以使用前序（中左右），也可以使用后序遍历（左右中），使用前序求的就是深度，使用后序求的是高度。

二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

下面代码为：递归（后序）

class Solution {
    public int maxDepth(TreeNode root) {
        int depth = 0;
        depth = invert(root);
        return depth;
    }
    // 1.返回值：当前节点（下面的）高度
    int invert(TreeNode node) {
        // 2.结束条件
        if(node == null) return 0;
        // 3.递归逻辑
        int left_depth = invert(node.left) + 1;
        int right_depth = invert(node.right) + 1;
        return Math.max(left_depth, right_depth);
    }
}

n叉树的最大深度

自己想法

递归法

class Solution {
    public int maxDepth(Node root) {
        int depth = 0;
        depth = invert(root);
        return depth;
    }
    // 1.返回值：当前节点下面的深度
    int invert(Node node) {
        // 2.结束条件
        if(node == null) return 0;
        // 3.递归逻辑
        int depth = 1;
        for (Node child : node.children){
            depth = Math.max(depth, invert(child) + 1);
        }
        return depth;
    }
}

111.二叉树的最小深度

自己想法

下面代码为：递归（前序）

class Solution {
    public int min_depth;
    public int minDepth(TreeNode root) {
        this.min_depth = -1;
        if(root == null) return 0;
        invert(root, 0);
        return this.min_depth;
    }
    // 1.返回值：空，因为用this.min_depth来记录了
    void invert(TreeNode node, int now_depth) {
        // 2.返回条件
        if(node == null) return;
        // 3.递归逻辑
        now_depth++;
        // 3.1.如果是叶子节点，那么和this.min_depth比较
        if(node.left == null && node.right == null) {
            if(this.min_depth == -1) this.min_depth = now_depth;
            else this.min_depth = Math.min(this.min_depth, now_depth);
        }
        // 3.2.如果不是叶子，那么走左右
        invert(node.left, now_depth);
        invert(node.right, now_depth);
    }
}

回顾

求高度，用后序遍历，递归返回的就是高度
求深度，用前序遍历，递归不返回，用参数来记录深度。如果需要找最小深度，那么需要用全局变量来记录最小深度

222.完全二叉树的节点个数

自己想法

直接递归，不仅适用于完全二叉树，也适用于普通二叉树。

时间复杂度：O(n)
空间复杂度：O(log n)，算上了递归系统栈占用的空间

class Solution {
    public int countNodes(TreeNode root) {
        return invert(root);
    }
    // 1.返回值：当前node下的节点数（包括自己）
    int invert(TreeNode node) {
        // 2.结束条件
        if(node == null) return 0;
        // 3.递归逻辑：当前node下的节点数等于左+右+1（自己）
        int left_nodes = invert(node.left);
        int right_nodes = invert(node.right);
        return left_nodes + right_nodes + 1;
    }
}

题解想法

利用完全二叉树的性质：满二叉树（特殊的完全二叉树）的结点数为：2^depth - 1

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

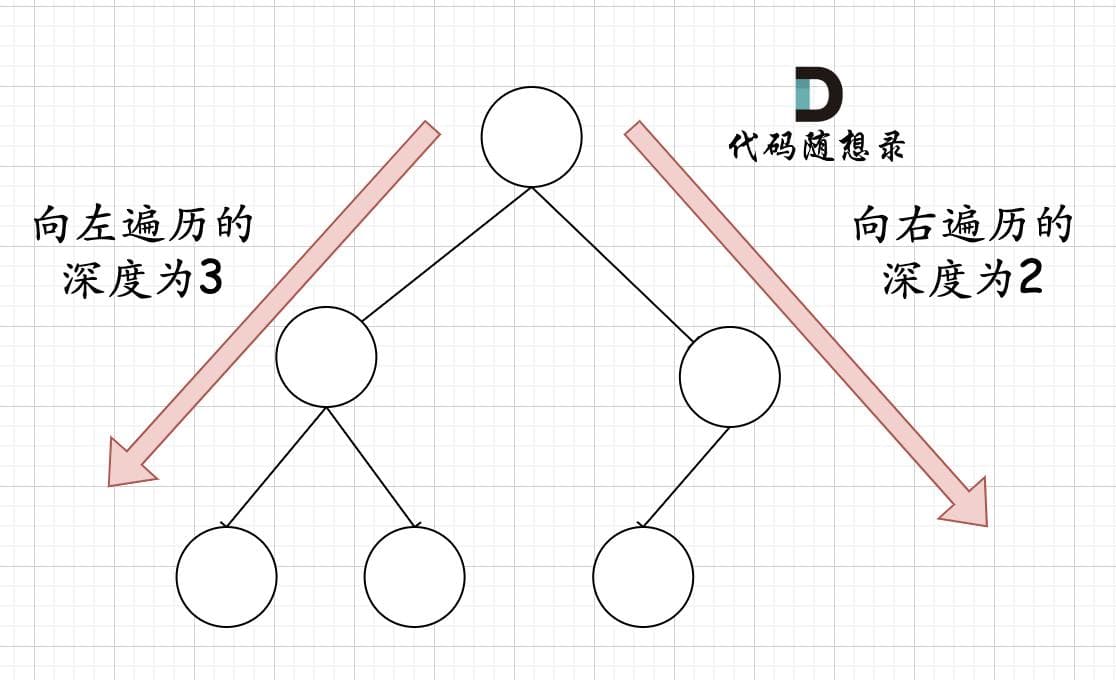
如何去判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树

时间复杂度：O(log n x log n)
空间复杂度：O(log n)

class Solution {
    public int countNodes(TreeNode root) {
        return invert(root);
    }
    // 1.返回值：当前node下的节点数（包括自己）
    int invert(TreeNode node) {
        // 2.结束条件
        if(node == null) return 0;
        // 3.递归逻辑：当前node下的节点数等于左+右+1（自己）
        // 3.1.判断左右分别是不是完全二叉树
        TreeNode left = node.left;
        TreeNode right = node.right;
        int left_depth = 0, right_depth = 0;
        while(left != null) {
            left = left.left;
            left_depth++;
        }
        while(right != null) {
            right = right.right;
            right_depth++;
        }
        // 3.2.是的话用公式计算
        if(left_depth == right_depth)
            return (2 << left_depth) - 1;  // 移位操作计算 2^left_depth-1
        // 3.3.不是的话继续递归
        return invert(node.left) + invert(node.right) + 1;
    }
}